Please see the general programming webpage for details about the programming environment for this course, guidelines for programming style, and details on electronic submission of assignments.
For this assignment, you may work with 1 partner in regard to the design and implementation of your project.
Please make sure you adhere to the policies on academic integrity in this regard.
The files you may need for this assignment can be downloaded here.
On computer systems, all of the underlying data is represented digitally as a sequence of bits (conventionally denoted as 0's and 1's). This is true for numbers, texts, images, sound, executables, and any other data that can be stored or transmitted digitally. Yet for a program to be able to utilize any such data, it must know how to interpret that sequence of bits. We typically call this process decoding.
For motivation, we consider the case of representing text strings digitally (though the techniques we discuss here apply easily to other forms of data as well). A traditionally way to represent text over a given alphabet is to have a distinct binary code for each character of the language. In English, the most common method is based on the use of ASCII (American Standard Code for Information Interchange). ASCII is an example of what is termed a fixed-length code in that the code for each character is the same number of bits; in particular, ASCII uses an 8-bit code. For example the code for the character "A" is 01000001; the code for the character "a" is 01100001. Obviously, it would be nice to use as few bits as possible to encode a long message, but the reason for ASCII using 8-bits per code is to ensure that there are enough different patterns for each character in the desired alphabet. Notice that with 8-bit codes, there are exactly 28 different possible patterns. If we look at each 8-bit pattern as if it were a binary number, we get an integer value anywhere from 0 (i.e., 00000000) up to 255 (i.e., 11111111). This provides enough codes for upper and lower cased versions of the 26 letters in the alphabet, as well as the ten numerals, various punctuations, spaces, newlines, tabs, and various other special characters.
The significance of ASCII is that it provides a standard we can rely upon. If I have a message that I am assured is encoded in ASCII, it is a very straight forward process to decode it. Starting at the beginning, I get the first 8 bits and then look up that pattern in the codebook to translated it to a character of text; then I translate the next 8 bits and so on. That said, there is nothing very special about the particular choice of which codes were assigned to which characters in ASCII; what is important is that a sender and receiver use the same code. If you were to make up your own code where "A" was assigned some other code, and "B" some other code, but you did not tell me what codes you used, I would have great difficulty in decoding your message.
That said, even for English text, there are two important reasons for considering other encodings. The first is encryption. We specifically uses ASCII as a standard so that others will be able to properly interpret our data. If our goal was to disguise the message for others, yet still make it meaningful for a friend, we might choose to have an alternate encoding that our friend knows about but others do not.
The second reason for considering other encodings is for the sake of compression. If possible, we would love to be able to represent the same information with fewer bits. This means it would take less disk space to store as well as less effort for sending through a network. Some compressions schemes save bits by losing quality (e.g. MP3 for audio); those are called lossy compression. However it is also possible to compress data in a lossless way by choosing the right encoding. This assignment explores a form of lossless compression.
As we mentioned above, ASCII is a fixed-length code (with 8 bits per character). We might reduce the overall size of a message for two reasons. First, the 8 bits are necessary in ASCII in order to have a pattern for 256 distinct characters. In some messages, perhaps not all of those characters are used, thus perhaps we could use less bits. But this is not going to help for larger messages with a rich use of characters. The key is to recognize that certain characters tend to occur much more often then others in a particular message. We can develop a coding scheme based on a tradeoff where more frequently used letters get shorter codes and less frequently used letters get longer codes. We call such a coding scheme variable-length.
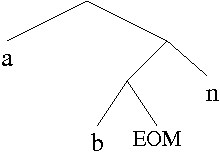
We will represent our code as a proper binary tree, with a leaf node for each character of the alphabet. The code for an individual character will be represented, from left-to-right, by tracing a path from the root to that leaf. For each step the path takes to a left-child we take a '0' and for each step to a right child we take a '1'. As an example, consider the following tree:

For technical reasons, our code include a special character EOM (end-of-message) to designate the end of an encoded message. We interpret the above tree as a code over the alphabet {a,b,n,EOM} with codes:
| Character | Our Code |
|---|---|
| a | 0 |
| b | 100 |
| EOM | 100 |
| n | 11 |
In a later assignment, we will explore how we might design a
tree which is optimized for the character frequency of a
particular message. For now, we consider things more from the
perspective of the decoder. To be able to read the message, someone
will need to be informed of the specific codes being used. With the
tree representation, decoding a message is rather straightforward.
The codes have a prefix-free property ensuring that one can
decode the message from left to right by repeatedly walking from the
root downward. Each
time we reach a leaf, we can output the character associated with that
leaf and then continue from the root. For example, with a message
1000110110101 in this example, we find:
1000110110101
ba na naEOM = banana
The reader must have a way to know when the message ends. One approach is to simply stop writing bits to the underlying file once the final character has been represented. Unfortunately, it is not quite this easy. Because of the architecture of a file system, file sizes must often be stored in larger blocks of bits, such as a byte. But a decoder cannot necessarily differentiate between final bits that are legitimate versus "junk". Therefore, we assume there is a special character in the alphabet which we denote as EOM. If we wanted to apend this character to ASCII, we would presumably want to give it a different code than all other characters. Since ASCII characters are coded from 0 to 255, a common choice for the EOM is to have it as 256. We adopt this convention, and therefore EOM has a natural nine-bit binary value (though we may assign it a different pattern in our encoding). We'll come back to this issue soon...
As mentioned earlier, for an encoded file to be useful for a reader, that reader must have knowledge of the specific code which is being used. A common approach for handling this issue is to simply place a representation of the tree itself as a header at the beginning of the message file; in this way, a reader is sure to have the code. Of course that tree representation must itself be represented at the lowest level as a sequence of zeros and ones. Since the goal is to minimize the overall number of bits, it is worthwhile trying to store the tree in as condensed a form as possible, so long as the reader can adequately reconstruct it.
Here is the approach we will use. If one were to perform a preorder traversal of a proper binary tree and furthermore were to output '0' when initially visiting each internal node, and '1' when initially visiting each external node, it turns out that this is sufficient information to be able to reconstruct the shape of the original tree. For example, the shape of the tree in the earlier diagram of this assignment would produce the pattern '0100111' in such a pre-order traversal (try it!).
Of course, we must represent not only the shape of the coding tree but also the underlying characters at the leaves (there is not relevant data for the internal nodes). Each leaf has a single character (or the special EOM character). To convey the choice of characters here, we will revert to using the original ASCII codes for each character -- however because the EOM requires a nine-bit code we will actually assume that we use an augmented nine-bit version of ASCII so that we can represent numbers from 0 to 256 (rather than 0 to 255).
Our precise file format is as follows. We perform an pre-order
traversal. For each internal node the file contains a '0'. For each
external node the file contains a '1' followed by an additional
nine bits which specify the character associated with that
leaf. Looking again at the earlier example of a tree, we represent it
as follows:
0100110000100100110001011000000001001101110
----a---- ----b---- ---EOF--- ----n----
In the end, the complete file contains the tree representation
followed by the encoded message, thus in this example:
01001100001001001100010110000000010011011101000110110101
----a---- ----b---- ---EOF--- ----n---- ba na naEOM = banana
Of course the color coding shown here is not really in the file. The
decode must infer the structure based upon the detailed conventions.
The end goal for this assignment is for you to write a decoder. It should prompt the user for the name of a compressed file (i.e., the combined tree and message). It should also prompt the user for the name of an output file in which the decoded message will be written.
You will clearly need to tackle the job in two stages:
Reconstruct the Tree
We will provide you with a fully-implemented Tree implementation
based upon our BinaryTree.h from class. But you must
start with a default tree (which is a single leaf) and expand
it according to the prescribed shape. Though you are not
required to use recursion, we strongly suggest that you view
recursion as a friend.
Think of the following. Read the first bit of the (sub)tree represenation. If it is a '1' then it is a single leaf: read the next nine bits which is the (extended) ASCII representation of the character. If that first bit had been a '0' then the current node should be internal. Therefore, it should be expanded, after which we recurse to build the left subtree and then the right subtree.
Decode the Message
Once the tree constructed, all of the remaining bits in the file
comprise the actual message. Read it bit-by-bit while
simulating walks from the root of the tree down to leaves,
outputing a character to the result each time you reach a leaf,
until you find the designated EOM character which ends the message.
All such files can be downloaded here.
For this assignment you must write your own top-level program; all of your code should go in a single file, decode.cpp, with the main routine starting out the process. Yet to aid your program, we are providing several exisiting classes for convenience.
BinaryTree.h
A definition and complete implementation of a BinaryTree class based
on our binary tree class from lecture. The only major modification is to
move several of the protected functions to the public section, such as
insertAsRightChild, createRoot, and others, so that you will be able to
use these functions to build your tree.
Bitstream.h, BitStreams.cpp
The standard input and output streams allow you to read data
from a file or to write data to a file, however they typically
demand that data be processed a byte at a time, rather than bit
by bit. For convenience, we provide corresponding stream
classes that support bitwise operations (for those interested,
our streams wrap the standard ones and buffer the byte-by-byte I/O).
InBitStream
Supports the following methods:
InBitStream()
New input stream object; though not usable yet until a file is opened.
bool open(filename)
Opens (or reopens) a file to be accessed via the
stream. Returns true if successful.
close()
Closes the underlying file.
int read()
Reads the next bit of the file. Returns either 0 or 1.
int read(int n)
Reads the next n bits of the file.
Returns those n bits as an integer value equivalent
to the associated n-bit binary number.
Should only be used when n is less than the
number of bits used to represent an int.
Once you've got those bits, you may do with them what you want. For example, if you've read 8 bits that you presume are an ASCII character you can cast using a syntax (char) i.
bool isOpen()
Returns true if stream is currently associated with an
open file.
bool eof()
Has end of underlying file been reached?
OutBitStream
Supports the following methods:
OutBitStream()
New output stream object; though not usable yet until a file is opened.
bool open(filename)
Opens (or reopens) a file to be accessed via the
stream. Returns true if successful.
close()
Closes the underlying file.
void write(int value)
Writes single bit to the file (assumes value is 0 or 1).
void write(int value, int n)
Writes n bits to the file. Those bits are described
by giving an integer value equivalent to the
associated n-bit binary number.
(it uses the least-significant n bits of the value,
though outputed from most to least significant).
bool isOpen()
Returns true if stream is currently associated with an
open file.
VariousExceptions.h
There are a variety of exception classes involved in this
assignment. Rather than define each in its own file, we've
bundled them all together for convenience.
makefile
This makefile should allow you to rebuild your project by
simply typing 'make' rather than in invoking the compiler
directly.
Consider an original message formatted as follows:
The coding tree we will use for this message appears as follows.This is a test. This is only a test. Testing, one, two three.
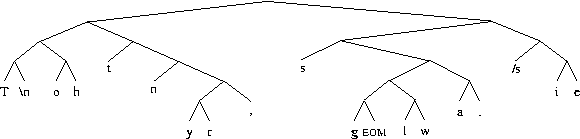
A preorder traversal of this tree, tagged with '0' for internal and '1' for external appears as: 0000110110101001110010001101101101011. Taking into consideration the insertion of 9-bit patterns for the character at each leaf, the full coding tree is represented as: The structure of this tree would be represented in binary as:
0000100101010010000010100100110111110011010000100111010001001101110001001111001100111001010001011000010011100110001001100111110000000001001101100100111011101001100001100010111001000100000010011010011001100101
----T---- ----\n--- ----o---- ----h---- ----t---- ----n---- ----y---- ----r---- ----,---- ----s---- ----g---- ---EOM--- ----l---- ----w---- ----a---- ----.---- ----\s--- ----i---- ----e----
With such a coding tree established, our original message is encoded beginning with,
000000111110100110111010011010110110010111110001010111
T h i s \s i s \s a \s t e s t .
We have created several other sample files for you to play with. They can either be downloaded here or accessed on turing directly from the input subdirectory of the project distribution. Here is a quick synopsis.
| filename | description | original size(bytes) | "compressed" size(bytes) | Compressed View |
|---|---|---|---|---|
| banana | the word 'banana' | 6 | 7 | view |
| testing | the preceding example | 62 | 57 | view |
| hwExample | the example given as a previous homework exercise | 28 | 36 | view |
| index.shtml | SHTML source for this program specification | 25971 | 15900 | |
| moby.txt | Moby Dick | 1221175 | 696916 |
decode.cpp
For simplicity, please put all of your code in a single file.
(you may declare whatever variables,
classes, function you wish within this single file).
Readme File
A brief summary of your program, and any further comments you
wish to make to the grader. If you do the extra credit, please
make this clear.
The assignment is worth 10 points. 1 point will be based on a checkpoint the Tuesday before the assignment is due; you will be expected to show me at least 20 lines of code by class time that day. The remaining 9 points will be based on your code working on all given examples, as well as proper commenting/indenting and the readme file.